User Guide

SPFlow is an open-source functional-oriented Python package for Probabilistic Circuits (PCs) with ready-to-use implementations for Sum-Product Networks (SPNs). PCs are a class of powerful deep probabilistic models - expressible as directed acyclic graphs - that allow for tractable querying. This library provides routines for creating, learning, manipulating and interacting with PCs and is highly extensible and customizable.

Create Toy Dataset

To demonstrate and visualize the main features of the library, we first create a 2D toy dataset with three Gaussian clusters, corresponding to labels 0, 1, and 2. The dataset is created with an imbalance. Therefore, class 0 has 200 datapoints, class 1 400 datapoints and class 2 600 datapoints, for a total of 1,200 data points.

import torch
import matplotlib.pyplot as plt
import numpy as np

# --- 1. Define the parameters for our dataset ---

n_points_per_cluster = 200

means = torch.tensor([
    [0.0, 3.0],  # Cluster 0
    [-3.0, -2.0],  # Cluster 1
    [3.0, -2.0]  # Cluster 2
])

stds = torch.tensor([
    [0.6, 0.6],
    [0.8, 0.4],
    [0.5, 0.7]
])

# --- 2. Generate the data and labels ---

all_clusters = []
all_labels = []

for i in range(means.shape[0]):
    samples = (torch.randn(n_points_per_cluster * (i + 1), 2) * stds[i]) + means[i]
    labels = torch.full((n_points_per_cluster * (i + 1),), i, dtype=torch.long)  # label = cluster index
    all_clusters.append(samples)
    all_labels.append(labels)

# Concatenate all data and labels
dataset = torch.cat(all_clusters)
labels = torch.cat(all_labels)

# --- 3. Shuffle dataset and labels together ---

shuffled_indices = torch.randperm(dataset.shape[0])
dataset = dataset[shuffled_indices]
labels = labels[shuffled_indices]

# --- 4. Display some info ---

print("Dataset successfully created.")
print(f"Shape of dataset: {dataset.shape}")
print(f"Shape of labels: {labels.shape}")
print("First 5 samples:")
print(dataset[:5])
print("Corresponding labels:")
print(labels[:5])

# --- 5. Visualize the labeled dataset ---

data_np = dataset.cpu().numpy()
labels_np = labels.cpu().numpy()


def plot_scatter(data_list, title=None, labels=None, label_list=None):
    colors = ["blue", "red", "yellow", "green"]
    plt.figure(figsize=(8, 6))
    for idx, data in enumerate(data_list):
        print(len(data_list))
        print(data.shape)
        print(label_list[idx])
        if labels is not None and len(data_list) == 1:
            plt.scatter(data[:, 0], data[:, 1], c=labels, cmap="viridis", s=10, alpha=0.7)
            plt.colorbar(label='Cluster Label')
        else:
            plt.scatter(data[:, 0], data[:, 1], c=colors[idx], s=10, alpha=0.7, label=label_list[idx])
            plt.legend()

    plt.title(title)
    plt.xlabel('Feature 1 (x-axis)')
    plt.ylabel('Feature 2 (y-axis)')
    plt.grid(True, linestyle='--', alpha=0.6)
    plt.axis('equal')
    #plt.colorbar(label='Cluster Label')

    plt.show()


plot_scatter([data_np], title='Generated 2D Toy Dataset (with Labels)', labels=labels_np, label_list=['Toy Data'])

Dataset successfully created.
Shape of dataset: torch.Size([1200, 2])
Shape of labels: torch.Size([1200])
First 5 samples:
tensor([[-3.2128, -1.8477],
        [ 0.8445,  3.5364],
        [ 0.5386,  2.2832],
        [ 1.1836,  2.6053],
        [ 3.0663, -1.3714]])
Corresponding labels:
tensor([1, 0, 0, 0, 2])
1
(1200, 2)
Toy Data

Model Configuration

The circuits you create with this library are modular.

All modules share the same base structure. Each module is defined by its number of output features and output channels. You can think of output features as the number of nodes with different scopes in one layer. You can think of output channels as how many times a node with the same scope is repeated in a layer. This structure lets you define simple nodes (with a shape of (1, 1)), node vectors along the feature (N, 1) or channel (1, M) dimension, or full leaf layers (N, M). In many cases, using layers instead of single nodes is much faster and more memory-efficient.

Each module also has an input attribute that points to its input module. This lets you stack modules together in any order.

Below, we will build a simple Sum-Product Network by stacking leaf, product, and sum layers.

from spflow.modules.leaves import Normal
from spflow.modules.sums import Sum
from spflow.modules.products import Product
from spflow.meta.data import Scope
from IPython.display import display, Image

scope = Scope([0, 1])

leaf_layer = Normal(scope=scope, out_channels=6)
product_layer = Product(inputs=leaf_layer)
spn = Sum(inputs=product_layer, out_channels=1)
spn

Sum(
  D=1, C=1, R=1, weights=(1, 6, 1, 1)
  (inputs): Product(
    D=1, C=6, R=1
    (inputs): Normal(D=2, C=6, R=1)
  )
)

Below is a visualization of the SPN defined above. The number of output channels of a sum or leaf layer is equivalent to the number of nodes in that layer. The number of nodes in a product layer is derived from the number of nodes in its input.

from pathlib import Path

guide_dir = Path('docs/source/guides') if Path('docs/source/guides').exists() else Path('.')
display(Image(filename=str(guide_dir / 'StandardSPN.png')))

Next, we can train the SPN, for example, using gradient descent. The library already provides a method for training an SPN with gradient descent. To do this, simply pass the module you want to train and the training parameters such as the number of epochs, learning rate, etc.

from spflow.learn import train_gradient_descent
from torch.utils.data import DataLoader, TensorDataset
import logging

logging.basicConfig(
    level=logging.INFO,
    format="%(asctime)s [%(levelname)s] %(name)s: %(message)s"
)

train_dataset = TensorDataset(dataset)
dataloader = DataLoader(train_dataset, batch_size=10)
train_gradient_descent(spn, dataloader, epochs=10, lr=0.1, verbose=True)

2026-03-02 08:08:22,625 [INFO] spflow.learn.gradient_descent: Epoch [0/10]: Loss: 3.025869607925415
2026-03-02 08:08:22,650 [INFO] spflow.learn.gradient_descent: Epoch [1/10]: Loss: 3.0339221954345703
2026-03-02 08:08:22,674 [INFO] spflow.learn.gradient_descent: Epoch [2/10]: Loss: 3.039278507232666
2026-03-02 08:08:22,697 [INFO] spflow.learn.gradient_descent: Epoch [3/10]: Loss: 3.034407377243042
2026-03-02 08:08:22,720 [INFO] spflow.learn.gradient_descent: Epoch [4/10]: Loss: 3.046787738800049
2026-03-02 08:08:22,743 [INFO] spflow.learn.gradient_descent: Epoch [5/10]: Loss: 3.209367275238037
2026-03-02 08:08:22,767 [INFO] spflow.learn.gradient_descent: Epoch [6/10]: Loss: 3.214216709136963
2026-03-02 08:08:22,791 [INFO] spflow.learn.gradient_descent: Epoch [7/10]: Loss: 3.2009239196777344
2026-03-02 08:08:22,814 [INFO] spflow.learn.gradient_descent: Epoch [8/10]: Loss: 3.1970839500427246
2026-03-02 08:08:22,837 [INFO] spflow.learn.gradient_descent: Epoch [9/10]: Loss: 3.1943774223327637

Once the SPN is trained, we can perform queries such as inference and sampling. SPFlow uses internal dispatching so that a single query function can work across all module types. For example, the log_likelihood method shown below can be used for every SPN model encountered throughout this guide.

ll = spn.log_likelihood(dataset)
ll

tensor([[[[-1.8440]]],


        [[[-4.1174]]],


        [[[-3.6423]]],


        ...,


        [[[-2.8012]]],


        [[[-3.2786]]],


        [[[-2.0993]]]], grad_fn=<LogsumexpBackward0>)

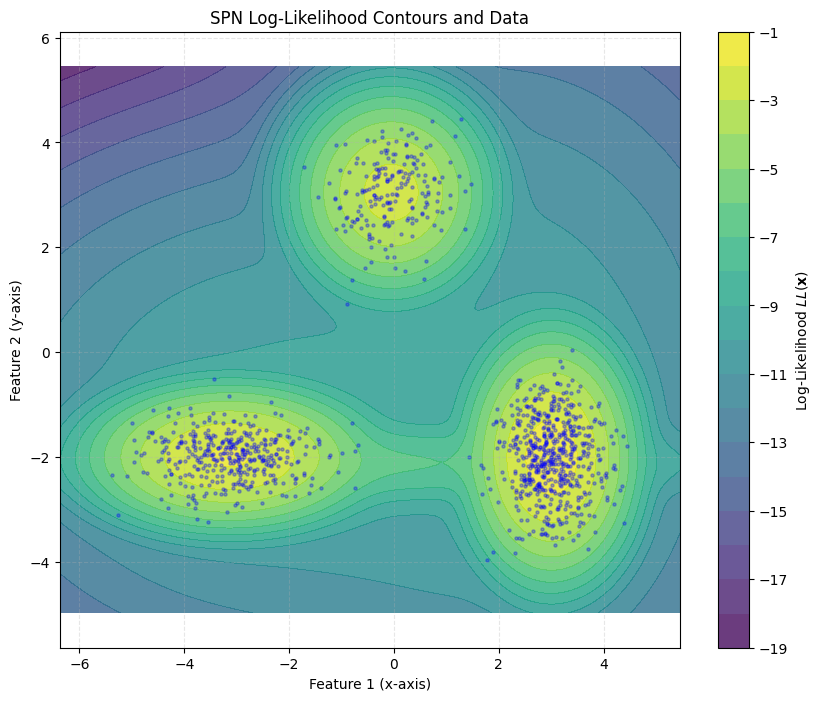
Finally, we can visualize the training results on our toy dataset.

data_np = dataset.cpu().numpy()


def plot_contour(data, spn):
    # Define the boundaries of the plot with a small padding
    x_min, x_max = data_np[:, 0].min() - 1, data_np[:, 0].max() + 1
    y_min, y_max = data_np[:, 1].min() - 1, data_np[:, 1].max() + 1

    # Create a grid of points
    grid_resolution = 200
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, grid_resolution),
                         np.linspace(y_min, y_max, grid_resolution))

    # Stack the grid points into a format our function can accept: [n_points, 2]
    grid_points = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
    ll = spn.log_likelihood(grid_points)
    # Reshape the LL values to match the grid shape for plotting
    Z = ll.detach().cpu().numpy().reshape(xx.shape)

    # --- 6. Visualize the Data and Log-Likelihood Contours ---

    plt.figure(figsize=(10, 8))

    # Plot the filled contour map of the log-likelihood
    # Higher values (brighter colors) mean the model thinks data is more likely there
    contour = plt.contourf(xx, yy, Z, levels=20, cmap='viridis', alpha=0.8)

    # Add a color bar to show the LL scale
    plt.colorbar(contour, label='Log-Likelihood $LL(\mathbf{x})$')

    # Overlay the scatter plot of the actual data points
    # We make them semi-transparent and small to see the density and contours
    plt.scatter(data_np[:, 0], data_np[:, 1], s=5, alpha=0.3, c='blue')

    # Add titles and labels
    plt.title('SPN Log-Likelihood Contours and Data')
    plt.xlabel('Feature 1 (x-axis)')
    plt.ylabel('Feature 2 (y-axis)')
    plt.grid(True, linestyle='--', alpha=0.3)
    plt.axis('equal')  # Ensures the scaling is the same on both axes
    plt.show()


plot_contour(data_np, spn)

<>:29: SyntaxWarning: invalid escape sequence '\m'
<>:29: SyntaxWarning: invalid escape sequence '\m'
/var/folders/t3/57fhyt955l9d7dby5dmlzs900000gn/T/ipykernel_18862/2429085685.py:29: SyntaxWarning: invalid escape sequence '\m'
  plt.colorbar(contour, label='Log-Likelihood $LL(\mathbf{x})$')

Temporary Method Replacement

SPFlow supports temporarily substituting module methods. For example, you can replace the sum operation in Sum with a custom implementation for a single call graph.

import torch
from spflow.modules.sums import Sum
from spflow.modules.products import Product
from spflow.modules.leaves import Normal
from spflow.meta import Scope
from spflow.utils import replace

torch.manual_seed(1)

# Create a probabilistic circuit: Product(Sum(Product(Normal)))
scope = Scope([0, 1])
normal = Normal(scope=scope, out_channels=4)
inner_product = Product(inputs=normal)
sum_module = Sum(inputs=inner_product, out_channels=1)
root_product = Product(inputs=sum_module)

# Create test data
data = torch.randn(3, 2)

# Normal inference
log_likelihood_original = root_product.log_likelihood(data).flatten()
print(f"Original log-likelihood: {log_likelihood_original}")

# Define a custom log_likelihood for Sum modules
def max_ll(self, data, cache=None):
    ll = self.inputs.log_likelihood(data, cache=cache).unsqueeze(3)
    weighted_lls = ll + self.log_weights.unsqueeze(0)
    return torch.max(weighted_lls, dim=self.sum_dim + 1)[0]

# Temporarily replace Sum.log_likelihood with custom implementation
with replace(Sum.log_likelihood, max_ll):
    log_likelihood_custom = root_product.log_likelihood(data).flatten()
    print(f"Custom log-likelihood:   {log_likelihood_custom}")

# Original method is automatically restored
log_likelihood_restored = root_product.log_likelihood(data).flatten()
print(f"Restored log-likelihood: {log_likelihood_restored}")

Original log-likelihood: tensor([-1.2842, -2.8750, -7.2442], grad_fn=<ViewBackward0>)
Custom log-likelihood:   tensor([-1.4334, -3.5256, -7.9031], grad_fn=<ViewBackward0>)
Restored log-likelihood: tensor([-1.2842, -2.8750, -7.2442], grad_fn=<ViewBackward0>)

Automatic Model creation

Besides creating an SPN manually by stacking layers, it is also possible to use algorithms to automatically construct the SPN architecture. This can make it easier to start using SPNs.

Rat-SPN

The Rat-SPN algorithm builds a deep network structure by recursively partitioning the features (variables) into random subsets and alternating between sum and product layers. Below, we set up a Rat-SPN by defining its structure and parameters.

from spflow.zoo.rat.rat_spn import RatSPN
from spflow.modules.ops.split import SplitMode

depth = 1
n_region_nodes = 3
num_leaves = 2
num_repetitions = 2
n_root_nodes = 1
num_feature = 2

scope = Scope(list(range(0, num_feature)))

rat_leaf_layer = Normal(scope=scope, out_channels=num_leaves, num_repetitions=num_repetitions)
rat = RatSPN(
    leaf_modules=[rat_leaf_layer],
    n_root_nodes=n_root_nodes,
    n_region_nodes=n_region_nodes,
    num_repetitions=num_repetitions,
    depth=depth,
    outer_product=True,
    split_mode=SplitMode.consecutive(),
)
print(rat.to_str())

RatSPN [D=1, C=1, R=2] → scope: 0-1
└─ RepetitionMixingLayer [D=1, C=1] [weights: (1, 1, 2)] → scope: 0-1
   └─ Sum [D=1, C=1] [weights: (1, 4, 1, 2)] → scope: 0-1
      └─ OuterProduct [D=1, C=4] → scope: 0-1
         └─ SplitConsecutive [D=2, C=2] → scope: 0-1
            └─ Factorize [D=2, C=2] → scope: 0-1
               └─ Normal [D=2, C=2] → scope: 0-1

Here is a visualization of the architecture we just created.

from pathlib import Path

guide_dir = Path('docs/source/guides') if Path('docs/source/guides').exists() else Path('.')
display(Image(filename=str(guide_dir / 'Rat_SPN.png')))

ll = rat.log_likelihood(dataset)
ll

tensor([[[[-10.0750]]],


        [[[ -7.0355]]],


        [[[ -4.5595]]],


        ...,


        [[[ -4.7323]]],


        [[[ -7.1262]]],


        [[[-15.8514]]]], grad_fn=<ViewBackward0>)

We can again train this model using the provided gradient descent method.

train_gradient_descent(rat, dataloader, epochs=20, lr=0.1)

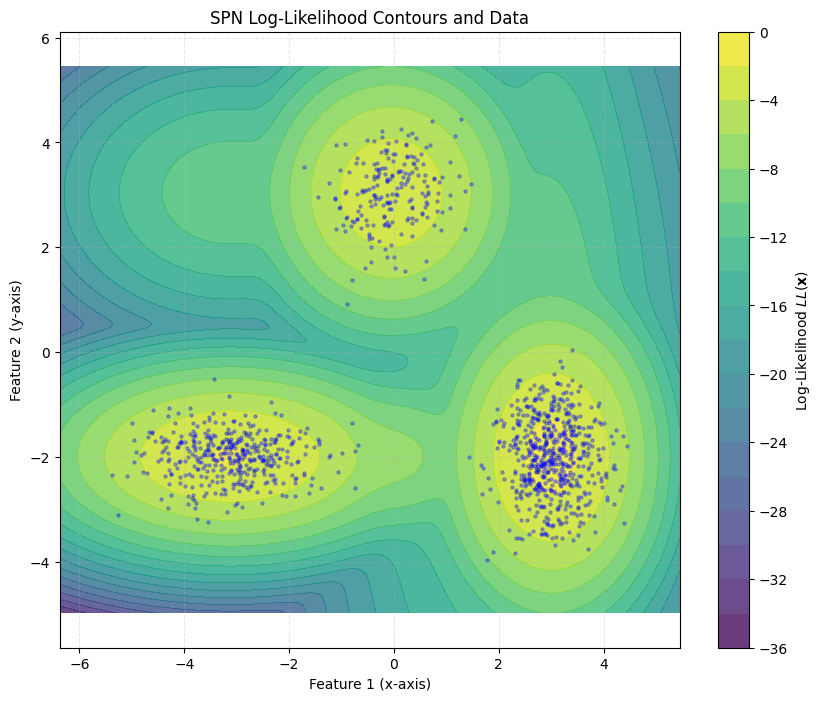
To verify that the training worked properly, we can visualize the log-likelihoods of the trained model.

data_np = dataset.cpu().numpy()
plot_contour(data_np, rat)

Of course, computing log-likelihoods is not the only thing the model can do. Below is a visualization of samples drawn from the trained Rat-SPN.

samples = spn.sample(num_samples=1500).detach().cpu().numpy()
plot_scatter([data_np, samples], title='Generated 2D Toy Dataset', label_list=['Original Data', 'Samples'])

2
(1200, 2)
Original Data
2
(1500, 2)
Samples

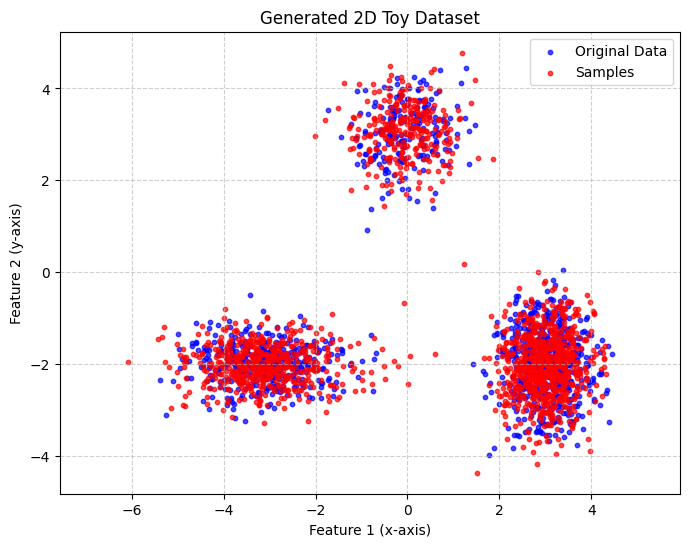
Up to now, we have focused only on generation, without considering the labels of the training instances. Next, we will train a second Rat-SPN for classification.

import logging

logging.basicConfig(
    level=logging.INFO,
    format="%(asctime)s [%(levelname)s] %(name)s: %(message)s"
)

depth = 1
n_region_nodes = 3
num_leaves = 3
num_repetitions = 1
n_root_nodes = 3
num_feature = 2

scope = Scope(list(range(0, num_feature)))

rat_leaf_layer = Normal(scope=scope, out_channels=num_leaves, num_repetitions=num_repetitions)
rat_class = RatSPN(
    leaf_modules=[rat_leaf_layer],
    n_root_nodes=n_root_nodes,
    n_region_nodes=n_region_nodes,
    num_repetitions=num_repetitions,
    depth=depth,
    outer_product=True,
    split_mode=SplitMode.consecutive(),
)
train_dataset = TensorDataset(dataset.clone(), labels.clone())

dataloader_with_labels = DataLoader(train_dataset, batch_size=10)

train_gradient_descent(rat_class, dataloader_with_labels, epochs=100, lr=0.1, is_classification=True,
                       verbose=True)

2026-03-02 08:08:24,237 [INFO] spflow.learn.gradient_descent: Epoch [0/100]: Loss: 2.148190498352051
2026-03-02 08:08:24,349 [INFO] spflow.learn.gradient_descent: Epoch [1/100]: Loss: 2.2462964057922363
2026-03-02 08:08:24,465 [INFO] spflow.learn.gradient_descent: Epoch [2/100]: Loss: 2.2065184116363525
2026-03-02 08:08:24,580 [INFO] spflow.learn.gradient_descent: Epoch [3/100]: Loss: 2.1779274940490723
2026-03-02 08:08:24,694 [INFO] spflow.learn.gradient_descent: Epoch [4/100]: Loss: 2.1533915996551514
2026-03-02 08:08:24,794 [INFO] spflow.learn.gradient_descent: Epoch [5/100]: Loss: 2.1403164863586426
2026-03-02 08:08:24,905 [INFO] spflow.learn.gradient_descent: Epoch [6/100]: Loss: 2.1278843879699707
2026-03-02 08:08:25,016 [INFO] spflow.learn.gradient_descent: Epoch [7/100]: Loss: 2.1193275451660156
2026-03-02 08:08:25,128 [INFO] spflow.learn.gradient_descent: Epoch [8/100]: Loss: 2.1121559143066406
2026-03-02 08:08:25,238 [INFO] spflow.learn.gradient_descent: Epoch [9/100]: Loss: 2.106269359588623
2026-03-02 08:08:25,340 [INFO] spflow.learn.gradient_descent: Epoch [10/100]: Loss: 2.101306676864624
2026-03-02 08:08:25,436 [INFO] spflow.learn.gradient_descent: Epoch [11/100]: Loss: 2.097092390060425
2026-03-02 08:08:25,527 [INFO] spflow.learn.gradient_descent: Epoch [12/100]: Loss: 2.0934925079345703
2026-03-02 08:08:25,617 [INFO] spflow.learn.gradient_descent: Epoch [13/100]: Loss: 2.090406894683838
2026-03-02 08:08:25,707 [INFO] spflow.learn.gradient_descent: Epoch [14/100]: Loss: 2.087754249572754
2026-03-02 08:08:25,796 [INFO] spflow.learn.gradient_descent: Epoch [15/100]: Loss: 2.0854692459106445
2026-03-02 08:08:25,891 [INFO] spflow.learn.gradient_descent: Epoch [16/100]: Loss: 2.0834946632385254
2026-03-02 08:08:25,981 [INFO] spflow.learn.gradient_descent: Epoch [17/100]: Loss: 2.0817856788635254
2026-03-02 08:08:26,071 [INFO] spflow.learn.gradient_descent: Epoch [18/100]: Loss: 2.0803024768829346
2026-03-02 08:08:26,162 [INFO] spflow.learn.gradient_descent: Epoch [19/100]: Loss: 2.079012870788574
2026-03-02 08:08:26,252 [INFO] spflow.learn.gradient_descent: Epoch [20/100]: Loss: 2.0778884887695312
2026-03-02 08:08:26,342 [INFO] spflow.learn.gradient_descent: Epoch [21/100]: Loss: 2.07690691947937
2026-03-02 08:08:26,438 [INFO] spflow.learn.gradient_descent: Epoch [22/100]: Loss: 2.076046943664551
2026-03-02 08:08:26,534 [INFO] spflow.learn.gradient_descent: Epoch [23/100]: Loss: 2.0752930641174316
2026-03-02 08:08:26,633 [INFO] spflow.learn.gradient_descent: Epoch [24/100]: Loss: 2.0746312141418457
2026-03-02 08:08:26,728 [INFO] spflow.learn.gradient_descent: Epoch [25/100]: Loss: 2.0740485191345215
2026-03-02 08:08:26,818 [INFO] spflow.learn.gradient_descent: Epoch [26/100]: Loss: 2.073535203933716
2026-03-02 08:08:26,912 [INFO] spflow.learn.gradient_descent: Epoch [27/100]: Loss: 2.073082447052002
2026-03-02 08:08:27,000 [INFO] spflow.learn.gradient_descent: Epoch [28/100]: Loss: 2.0726823806762695
2026-03-02 08:08:27,088 [INFO] spflow.learn.gradient_descent: Epoch [29/100]: Loss: 2.0723280906677246
2026-03-02 08:08:27,176 [INFO] spflow.learn.gradient_descent: Epoch [30/100]: Loss: 2.072014808654785
2026-03-02 08:08:27,264 [INFO] spflow.learn.gradient_descent: Epoch [31/100]: Loss: 2.071737051010132
2026-03-02 08:08:27,353 [INFO] spflow.learn.gradient_descent: Epoch [32/100]: Loss: 2.07149076461792
2026-03-02 08:08:27,441 [INFO] spflow.learn.gradient_descent: Epoch [33/100]: Loss: 2.071272373199463
2026-03-02 08:08:27,529 [INFO] spflow.learn.gradient_descent: Epoch [34/100]: Loss: 2.071077823638916
2026-03-02 08:08:27,624 [INFO] spflow.learn.gradient_descent: Epoch [35/100]: Loss: 2.0709052085876465
2026-03-02 08:08:27,725 [INFO] spflow.learn.gradient_descent: Epoch [36/100]: Loss: 2.070751667022705
2026-03-02 08:08:27,825 [INFO] spflow.learn.gradient_descent: Epoch [37/100]: Loss: 2.070615291595459
2026-03-02 08:08:27,926 [INFO] spflow.learn.gradient_descent: Epoch [38/100]: Loss: 2.0704939365386963
2026-03-02 08:08:28,021 [INFO] spflow.learn.gradient_descent: Epoch [39/100]: Loss: 2.070385456085205
2026-03-02 08:08:28,122 [INFO] spflow.learn.gradient_descent: Epoch [40/100]: Loss: 2.070289134979248
2026-03-02 08:08:28,218 [INFO] spflow.learn.gradient_descent: Epoch [41/100]: Loss: 2.0702037811279297
2026-03-02 08:08:28,315 [INFO] spflow.learn.gradient_descent: Epoch [42/100]: Loss: 2.070127487182617
2026-03-02 08:08:28,415 [INFO] spflow.learn.gradient_descent: Epoch [43/100]: Loss: 2.070059061050415
2026-03-02 08:08:28,510 [INFO] spflow.learn.gradient_descent: Epoch [44/100]: Loss: 2.069998264312744
2026-03-02 08:08:28,607 [INFO] spflow.learn.gradient_descent: Epoch [45/100]: Loss: 2.06994366645813
2026-03-02 08:08:28,699 [INFO] spflow.learn.gradient_descent: Epoch [46/100]: Loss: 2.0698959827423096
2026-03-02 08:08:28,788 [INFO] spflow.learn.gradient_descent: Epoch [47/100]: Loss: 2.069852828979492
2026-03-02 08:08:28,877 [INFO] spflow.learn.gradient_descent: Epoch [48/100]: Loss: 2.0698142051696777
2026-03-02 08:08:28,980 [INFO] spflow.learn.gradient_descent: Epoch [49/100]: Loss: 2.069779872894287
2026-03-02 08:08:29,088 [INFO] spflow.learn.gradient_descent: Epoch [50/100]: Loss: 2.2302005290985107
2026-03-02 08:08:29,181 [INFO] spflow.learn.gradient_descent: Epoch [51/100]: Loss: 2.2324790954589844
2026-03-02 08:08:29,276 [INFO] spflow.learn.gradient_descent: Epoch [52/100]: Loss: 2.2308449745178223
2026-03-02 08:08:29,368 [INFO] spflow.learn.gradient_descent: Epoch [53/100]: Loss: 2.229677200317383
2026-03-02 08:08:29,482 [INFO] spflow.learn.gradient_descent: Epoch [54/100]: Loss: 2.2287371158599854
2026-03-02 08:08:29,589 [INFO] spflow.learn.gradient_descent: Epoch [55/100]: Loss: 2.2279462814331055
2026-03-02 08:08:29,691 [INFO] spflow.learn.gradient_descent: Epoch [56/100]: Loss: 2.227271318435669
2026-03-02 08:08:29,796 [INFO] spflow.learn.gradient_descent: Epoch [57/100]: Loss: 2.2266876697540283
2026-03-02 08:08:29,913 [INFO] spflow.learn.gradient_descent: Epoch [58/100]: Loss: 2.2261812686920166
2026-03-02 08:08:30,009 [INFO] spflow.learn.gradient_descent: Epoch [59/100]: Loss: 2.2257347106933594
2026-03-02 08:08:30,103 [INFO] spflow.learn.gradient_descent: Epoch [60/100]: Loss: 2.225341320037842
2026-03-02 08:08:30,203 [INFO] spflow.learn.gradient_descent: Epoch [61/100]: Loss: 2.2249932289123535
2026-03-02 08:08:30,293 [INFO] spflow.learn.gradient_descent: Epoch [62/100]: Loss: 2.224682331085205
2026-03-02 08:08:30,393 [INFO] spflow.learn.gradient_descent: Epoch [63/100]: Loss: 2.2244043350219727
2026-03-02 08:08:30,482 [INFO] spflow.learn.gradient_descent: Epoch [64/100]: Loss: 2.2241549491882324
2026-03-02 08:08:30,572 [INFO] spflow.learn.gradient_descent: Epoch [65/100]: Loss: 2.223930835723877
2026-03-02 08:08:30,669 [INFO] spflow.learn.gradient_descent: Epoch [66/100]: Loss: 2.223729372024536
2026-03-02 08:08:30,760 [INFO] spflow.learn.gradient_descent: Epoch [67/100]: Loss: 2.2235474586486816
2026-03-02 08:08:30,850 [INFO] spflow.learn.gradient_descent: Epoch [68/100]: Loss: 2.2233834266662598
2026-03-02 08:08:30,951 [INFO] spflow.learn.gradient_descent: Epoch [69/100]: Loss: 2.223233699798584
2026-03-02 08:08:31,059 [INFO] spflow.learn.gradient_descent: Epoch [70/100]: Loss: 2.2230985164642334
2026-03-02 08:08:31,168 [INFO] spflow.learn.gradient_descent: Epoch [71/100]: Loss: 2.222975730895996
2026-03-02 08:08:31,275 [INFO] spflow.learn.gradient_descent: Epoch [72/100]: Loss: 2.2228641510009766
2026-03-02 08:08:31,379 [INFO] spflow.learn.gradient_descent: Epoch [73/100]: Loss: 2.222761869430542
2026-03-02 08:08:31,482 [INFO] spflow.learn.gradient_descent: Epoch [74/100]: Loss: 2.2226688861846924
2026-03-02 08:08:31,590 [INFO] spflow.learn.gradient_descent: Epoch [75/100]: Loss: 2.2077298164367676
2026-03-02 08:08:31,695 [INFO] spflow.learn.gradient_descent: Epoch [76/100]: Loss: 2.2022886276245117
2026-03-02 08:08:31,806 [INFO] spflow.learn.gradient_descent: Epoch [77/100]: Loss: 2.1984667778015137
2026-03-02 08:08:31,912 [INFO] spflow.learn.gradient_descent: Epoch [78/100]: Loss: 2.195736885070801
2026-03-02 08:08:32,020 [INFO] spflow.learn.gradient_descent: Epoch [79/100]: Loss: 2.1937618255615234
2026-03-02 08:08:32,127 [INFO] spflow.learn.gradient_descent: Epoch [80/100]: Loss: 2.1923179626464844
2026-03-02 08:08:32,230 [INFO] spflow.learn.gradient_descent: Epoch [81/100]: Loss: 2.1912522315979004
2026-03-02 08:08:32,333 [INFO] spflow.learn.gradient_descent: Epoch [82/100]: Loss: 2.190457820892334
2026-03-02 08:08:32,444 [INFO] spflow.learn.gradient_descent: Epoch [83/100]: Loss: 2.189859390258789
2026-03-02 08:08:32,545 [INFO] spflow.learn.gradient_descent: Epoch [84/100]: Loss: 2.1894030570983887
2026-03-02 08:08:32,637 [INFO] spflow.learn.gradient_descent: Epoch [85/100]: Loss: 2.1890511512756348
2026-03-02 08:08:32,731 [INFO] spflow.learn.gradient_descent: Epoch [86/100]: Loss: 2.1887741088867188
2026-03-02 08:08:32,832 [INFO] spflow.learn.gradient_descent: Epoch [87/100]: Loss: 2.188553810119629
2026-03-02 08:08:32,940 [INFO] spflow.learn.gradient_descent: Epoch [88/100]: Loss: 2.1883721351623535
2026-03-02 08:08:33,051 [INFO] spflow.learn.gradient_descent: Epoch [89/100]: Loss: 2.188220977783203
2026-03-02 08:08:33,163 [INFO] spflow.learn.gradient_descent: Epoch [90/100]: Loss: 2.18809175491333
2026-03-02 08:08:33,268 [INFO] spflow.learn.gradient_descent: Epoch [91/100]: Loss: 2.187978744506836
2026-03-02 08:08:33,374 [INFO] spflow.learn.gradient_descent: Epoch [92/100]: Loss: 2.1878762245178223
2026-03-02 08:08:33,484 [INFO] spflow.learn.gradient_descent: Epoch [93/100]: Loss: 2.187784194946289
2026-03-02 08:08:33,591 [INFO] spflow.learn.gradient_descent: Epoch [94/100]: Loss: 2.1876988410949707
2026-03-02 08:08:33,693 [INFO] spflow.learn.gradient_descent: Epoch [95/100]: Loss: 2.187619924545288
2026-03-02 08:08:33,801 [INFO] spflow.learn.gradient_descent: Epoch [96/100]: Loss: 2.1875429153442383
2026-03-02 08:08:33,908 [INFO] spflow.learn.gradient_descent: Epoch [97/100]: Loss: 2.187469482421875
2026-03-02 08:08:34,020 [INFO] spflow.learn.gradient_descent: Epoch [98/100]: Loss: 2.1873998641967773
2026-03-02 08:08:34,128 [INFO] spflow.learn.gradient_descent: Epoch [99/100]: Loss: 2.187331199645996

With this SPN, we can now draw samples based on its labels. Therefore, we use a sampling context. This sampling context can be passed to any sampling method. With the context, you can explicitly define from which output channel you want to sample or, for example, provide evidence. This allows advanced control over the sampling routine. In this case, the root layer has three output channels which correspond to the three classes. So being able to define from which output channel we want to sample means being able to choose from which class we want to sample.

from spflow.utils.cache import Cache
from spflow.utils.sampling_context import SamplingContext

num_features = 2

def sample_class(model, num_samples: int, class_idx: int):
    evidence = torch.full((num_samples, num_features), torch.nan)
    sampling_ctx = SamplingContext(
        channel_index=torch.full((num_samples, 1), class_idx, dtype=torch.int64),
        mask=torch.full((num_samples, 1), True, dtype=torch.bool),
    )
    return model.root_node.inputs._sample(data=evidence, sampling_ctx=sampling_ctx, cache=Cache())

samples_class0 = sample_class(rat_class, num_samples=200, class_idx=0).detach().cpu().numpy()
samples_class1 = sample_class(rat_class, num_samples=400, class_idx=1).detach().cpu().numpy()
samples_class2 = sample_class(rat_class, num_samples=600, class_idx=2).detach().cpu().numpy()

plot_scatter([data_np, samples_class0, samples_class1, samples_class2], title='Class-Conditional Samples',
             label_list=['Original Data', 'Samples Class 0', 'Samples Class 1', 'Samples Class 2'])

4
(1200, 2)
Original Data
4
(200, 2)
Samples Class 0
4
(400, 2)
Samples Class 1
4
(600, 2)
Samples Class 2

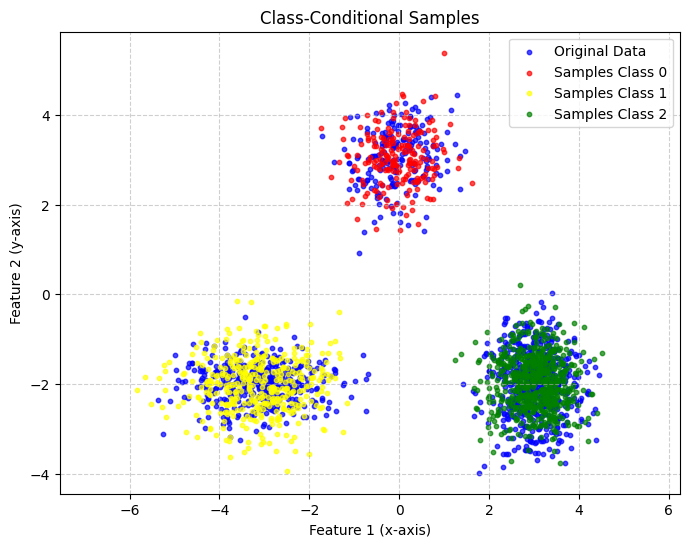
However, the model can of course also be used for classification. As an example, we visualize the trained decision boundaries of our model

import torch
import matplotlib.pyplot as plt
import numpy as np

# --- Assuming your dataset and labels are already created as above ---

# Let's assume you have an SPN model trained on this data:
# For example:
# spn = MySPNModel()
# spn.fit(dataset, labels)

# --- 1. Create a grid of points over the feature space ---
x_min, x_max = dataset[:, 0].min() - 1, dataset[:, 0].max() + 1
y_min, y_max = dataset[:, 1].min() - 1, dataset[:, 1].max() + 1

xx, yy = torch.meshgrid(
    torch.linspace(x_min, x_max, 300),
    torch.linspace(y_min, y_max, 300),
    indexing='xy'
)
grid_points = torch.stack([xx.flatten(), yy.flatten()], dim=1)

# --- 2. Get SPN predictions (probabilities or class scores) ---
# Example: if your SPN returns class probabilities
with torch.no_grad():
    probs = rat_class.log_posterior(grid_points)  # shape: [N_grid, num_classes]
    preds = probs.argmax(dim=-1)

# --- 3. Reshape predictions to match the grid ---
Z = preds.reshape(xx.shape)

# --- 4. Plot decision boundaries ---
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, levels=len(means), cmap="viridis")

# Plot the original data
plt.scatter(dataset[:, 0], dataset[:, 1], c=labels, cmap="viridis", s=10, edgecolor="k")

plt.title("SPN Classification Boundaries")
plt.xlabel("X₁")
plt.ylabel("X₂")
plt.show()

LearnSPN

Instead of creating a random structure, we can also train the SPN structure using the LearnSPN.

from spflow.learn.learn_spn import learn_spn

scope = Scope(list(range(2)))
normal_layer = Normal(scope=scope, out_channels=4)
learn_spn_model = learn_spn(
    torch.tensor(dataset, dtype=torch.float32),
    leaf_modules=normal_layer,
    out_channels=1,
    min_instances_slice=20,
    min_features_slice=2,
)
learn_spn

/var/folders/t3/57fhyt955l9d7dby5dmlzs900000gn/T/ipykernel_18862/522578384.py:6: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.detach().clone() or sourceTensor.detach().clone().requires_grad_(True), rather than torch.tensor(sourceTensor).
  torch.tensor(dataset, dtype=torch.float32),

<function spflow.learn.learn_spn.learn_spn(data: torch.Tensor, leaf_modules: list[spflow.modules.leaves.leaf.LeafModule] | spflow.modules.leaves.leaf.LeafModule, out_channels: int = 1, min_features_slice: int = 2, min_instances_slice: int = 100, scope=None, clustering_method: str | collections.abc.Callable = 'kmeans', partitioning_method: str | collections.abc.Callable = 'rdc', clustering_args: dict[str, typing.Any] | None = None, partitioning_args: dict[str, typing.Any] | None = None, full_data: torch.Tensor | None = None) -> spflow.modules.module.Module>

The trained SPN can now be used just like any other module

learn_spn_samples = learn_spn_model.sample(num_samples=1500).detach().cpu().numpy()
plot_scatter([data_np, learn_spn_samples], title='Generated 2D Toy Dataset', label_list=['Original Data', 'Samples'])

2
(1200, 2)
Original Data
2
(1500, 2)
Samples

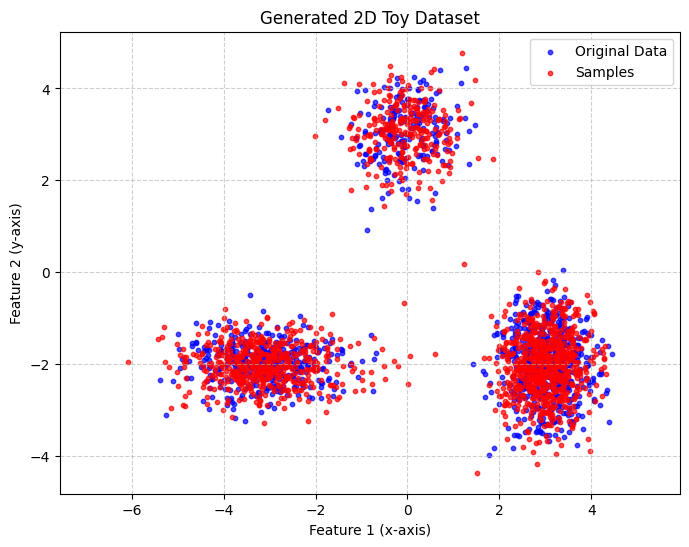
Advanced Queries

To showcase more advanced queries like conditional sampling and MPE (Most Probable Explanation) we take a look at a dataset with more features. Below, we load the digits dataset. This dataset contains 1797 8x8 images of digits 0 to 9.

import matplotlib.pyplot as plt

from sklearn import datasets

# Load the digits dataset
digits = datasets.load_digits()

# Display the last digit
plt.figure(1, figsize=(3, 3))
plt.imshow(digits.images[0], cmap=plt.cm.gray_r, interpolation="nearest")
plt.show()

X = digits.data  # shape (1797, 64)
y = digits.target  # shape (1797,)

X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long)

dataset = TensorDataset(X_tensor, y_tensor)
dataloader = DataLoader(dataset, batch_size=128, shuffle=True)

print(X_tensor.shape)
print(X_tensor.min(), X_tensor.max())

torch.Size([1797, 64])
tensor(0.) tensor(16.)

Again we create a Rat SPN, but this time we use a Binomial distribution for the leaf layer.

from spflow.modules.leaves import Binomial

depth = 3
n_region_nodes = 5
num_leaves = 5
num_repetitions = 2
n_root_nodes = 1
num_feature = 64
n = torch.tensor(16)  # total count for binomial distribution

scope = Scope(list(range(0, num_feature)))

rat_leaf_layer = Binomial(scope=scope, total_count=n, out_channels=num_leaves, num_repetitions=num_repetitions)
rat = RatSPN(
    leaf_modules=[rat_leaf_layer],
    n_root_nodes=n_root_nodes,
    n_region_nodes=n_region_nodes,
    num_repetitions=num_repetitions,
    depth=depth,
    outer_product=True,
    split_mode=SplitMode.consecutive(),
)
print(rat.to_str())

RatSPN [D=1, C=1, R=2] → scope: 0-63
└─ RepetitionMixingLayer [D=1, C=1] [weights: (1, 1, 2)] → scope: 0-63
   └─ Sum [D=1, C=1] [weights: (1, 25, 1, 2)] → scope: 0-63
      └─ OuterProduct [D=1, C=25] → scope: 0-63
         └─ SplitConsecutive [D=2, C=5] → scope: 0-63
            └─ Sum [D=2, C=5] [weights: (2, 25, 5, 2)] → scope: 0-63
               └─ OuterProduct [D=2, C=25] → scope: 0-63
                  └─ SplitConsecutive [D=4, C=5] → scope: 0-63
                     └─ Sum [D=4, C=5] [weights: (4, 25, 5, 2)] → scope: 0-63
                        └─ OuterProduct [D=4, C=25] → scope: 0-63
                           └─ SplitConsecutive [D=8, C=5] → scope: 0-63
                              └─ Factorize [D=8, C=5] → scope: 0-63
                                 └─ Binomial [D=64, C=5] → scope: 0-63

train_gradient_descent(rat, dataloader, epochs=20, lr=0.1)

Below is a visualization of some samples drawn from the Spn

samples = rat.sample(num_samples=5)
print(samples.shape)

for i in range(5):
    img = samples[i].reshape(8, 8)  # reshape back to 2D
    plt.subplot(1, 5, i + 1)
    plt.imshow(img, cmap="gray")
    plt.axis("off")
plt.show()

torch.Size([5, 64])

Now can show some more advanced queries. One of them is getting the MPE. It returns the most probable state of the probabilistic circuit. This is often helpful to generate more clear samples and a good indicator whether the model could learn the data or not, which is not always evident with regular samples.

mpe = rat.sample(num_samples=1, is_mpe=True)
plt.imshow(mpe.reshape(8, 8), cmap="gray")
plt.show()

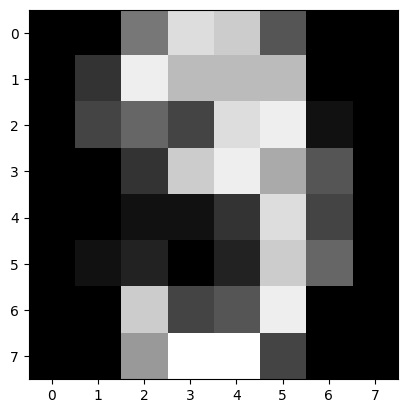
And at last we want to sample, given some evidence. In this example, the lower half of the image is given, and we want to sample the upper half given the lower half. This time, instead of explicitly defining a sampling context, we use the sample_with_evidence method. The method allows the user to just input the evidence and let the library internally handle the creation of the sampling context. This becomes handy if you have evidence but not multiple channel to sample from.

evidence = X_tensor[0]
evidence[:32] = torch.nan
plt.imshow(evidence.reshape(8, 8), cmap="gray")
plt.show()
evidence = evidence.unsqueeze(0)
print(evidence.shape)
samples = rat.sample_with_evidence(evidence=evidence)
plt.imshow(samples.reshape(8, 8), cmap="gray")
plt.show()

torch.Size([1, 64])

Regression via MPE (continuous target)

In SPFlow, you can model regression as a joint density p(y, x) (where y is continuous). After training by maximizing log-likelihood, you can predict with MPE:

• Build an evidence tensor where the input features x are set.

• Set the target y to NaN.

• Call model.mpe(data=evidence) to fill in the most probable y.

Below is a minimal example that learns p(y, x) = p(x) p(y|x) and evaluates prediction quality with MSE.

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
from torch import nn
from torch.utils.data import DataLoader, TensorDataset

from spflow.learn import train_gradient_descent
from spflow.meta import Scope
from spflow.modules.leaves import Normal
from spflow.modules.products import Product

torch.manual_seed(0)


def make_data(num_samples: int) -> torch.Tensor:
    x = (torch.rand(num_samples, 3) * 4.0) - 2.0
    y = (
        torch.sin(x[:, 0:1])
        + 0.05 * x[:, 1:2].pow(2)
        - 0.025 * x[:, 2:3]
        + 0.20 * torch.randn(num_samples, 1)
    )
    return torch.cat([y, x], dim=1).to(torch.float32)


train_data = make_data(800)  # columns: [y, x1, x2, x3]
test_data = make_data(200)


class ConditionalNormalParams(nn.Module):
    def __init__(self, in_features: int, hidden_features: int = 32) -> None:
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(in_features, hidden_features),
            nn.Tanh(),
            nn.Linear(hidden_features, 2),
        )

    def forward(self, evidence: torch.Tensor) -> dict[str, torch.Tensor]:
        out = self.net(evidence)
        loc = out[:, 0:1]
        raw_scale = out[:, 1:2]
        scale = F.softplus(raw_scale) + 1e-3
        return {
            "loc": loc.unsqueeze(2).unsqueeze(-1),
            "scale": scale.unsqueeze(2).unsqueeze(-1),
        }


# Joint model p(y, x) = p(x) * p(y|x)
y_given_x = Normal(
    scope=Scope(query=[0], evidence=[1, 2, 3]),
    out_channels=1,
    num_repetitions=1,
    parameter_fn=ConditionalNormalParams(in_features=3),
)
x_marginal = Normal(scope=Scope(query=[1, 2, 3]), out_channels=1, num_repetitions=1)
model = Product(inputs=[y_given_x, x_marginal])


@torch.no_grad()
def predict_y_mpe(model, data: torch.Tensor) -> torch.Tensor:
    evidence = data.clone()
    evidence[:, 0] = torch.nan
    return model.mpe(data=evidence)[:, 0]


@torch.no_grad()
def regression_mse(model, data: torch.Tensor) -> torch.Tensor:
    y_pred = predict_y_mpe(model, data)
    return torch.mean((y_pred - data[:, 0]).pow(2))


print("MSE before:", float(regression_mse(model, test_data)))

loader = DataLoader(TensorDataset(train_data), batch_size=64, shuffle=True)
train_gradient_descent(model, loader, epochs=20, lr=0.05)

print("MSE after:", float(regression_mse(model, test_data)))

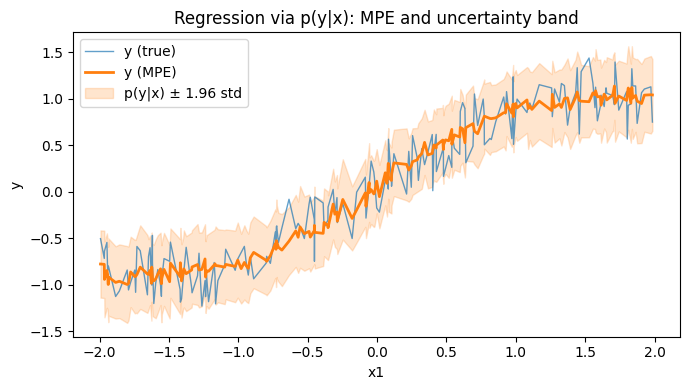
# Plot conditional distribution p(y|x) (±1 std) and the MPE prediction, as a function of x1
x1 = test_data[:, 1].detach().cpu()
y_true = test_data[:, 0].detach().cpu()

# Conditional distribution parameters for y|x come from the conditional leaf
x_evidence = test_data[:, [1, 2, 3]]
dist_y_given_x = y_given_x.conditional_distribution(x_evidence)

y_mpe = predict_y_mpe(model, test_data).detach().cpu()
y_std = dist_y_given_x.stddev.detach().cpu().squeeze()

order = torch.argsort(x1)
x1_sorted = x1[order]
y_true_sorted = y_true[order]
y_mpe_sorted = y_mpe[order]
y_std_sorted = y_std[order]

plt.figure(figsize=(7, 4))
plt.scatter(x1_sorted, y_true_sorted, linewidth=1.0, alpha=0.7, label="$y$ (true)", s=10)
mpe_line = plt.scatter(x1_sorted, y_mpe_sorted, linewidth=1.0, label="$\\hat{y}$ (MPE)", s=10)
mpe_color = mpe_line.get_facecolor()
plt.fill_between(
    x1_sorted,
    (y_mpe_sorted - 1.96 * y_std_sorted),
    (y_mpe_sorted + 1.96 * y_std_sorted),
    color=mpe_color,
    alpha=0.2,
    label="$p(y|x) ± 1.96$ std",
)
plt.xlabel("x1")
plt.ylabel("y")
plt.title("Regression via $p(y|x)$: MPE and uncertainty band")
plt.legend()
plt.tight_layout()
plt.show()

MSE before: 0.8204181790351868
MSE after: 0.04302353784441948