Composing SPNs from Sums and Products

The alternative to the DSL is to construct SPNs directly from Sum and Product objects, demonstrated here:

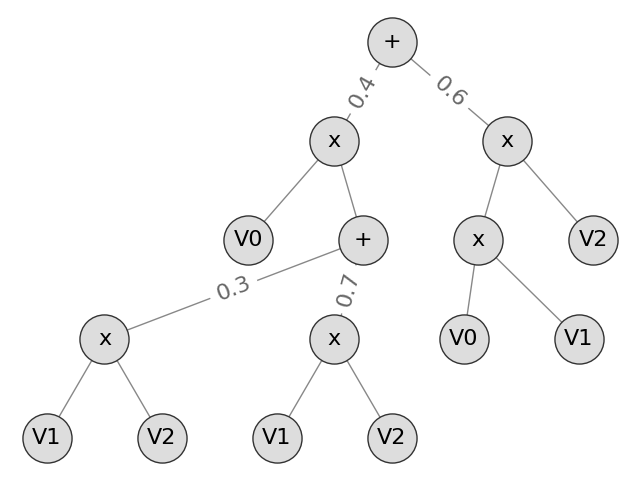
from spn.structure.leaves.parametric.Parametric import Categorical
from spn.structure.Base import Sum, Product
from spn.structure.Base import assign_ids, rebuild_scopes_bottom_up

from spn.io.Graphics import draw_spn
import matplotlib.pyplot as plt


p0 = Product(children=[Categorical(p=[0.3, 0.7], scope=1), Categorical(p=[0.4, 0.6], scope=2)])
p1 = Product(children=[Categorical(p=[0.5, 0.5], scope=1), Categorical(p=[0.6, 0.4], scope=2)])
s1 = Sum(weights=[0.3, 0.7], children=[p0, p1])
p2 = Product(children=[Categorical(p=[0.2, 0.8], scope=0), s1])
p3 = Product(children=[Categorical(p=[0.2, 0.8], scope=0), Categorical(p=[0.3, 0.7], scope=1)])
p4 = Product(children=[p3, Categorical(p=[0.4, 0.6], scope=2)])
spn = Sum(weights=[0.4, 0.6], children=[p2, p4])

assign_ids(spn)
rebuild_scopes_bottom_up(spn)

ax = draw_spn(spn)